Linear Algebra & C++: The Jacobi Method

Concepts

The Jacobi Method

For each \(k \geq 1\), generate the components \(x_{i}^{(k)}\) of \(x^{(k)}\) from \(x^{(k-1)}\) by

\[x_{i}^{(k)} = \frac{1}{a_{ii}}\left[\sum_{j=1, \\ j \neq i}^{n} (-a_{ij}x_{j}^{(k-1)}) + b_{i} \right]\text{, for } i=1,2, \cdots, n\]

Questions

Question 1

Solve the system of equations using Jacobi Iteration Method.

\[\begin{cases} 5x-2y+3z=-1 \\ -3x+9y+z=2 \\ 2x-y-7z=3 \end{cases}\]

Answers

Answer 1

#include <iostream>
#include <math.h>

#define f1(x, y, z) (-1+2*y-3*z)/5
#define f2(x, y, z) (2+3*x-z)/9
#define f3(x, y, z) (-3+2*x-y)/7

using namespace std;

int main(void) {
    double error;
    double xi=0, yi=0, zi=0;
    double xf, yf, zf;
    double error1, error2, error3;
    int count = 1;

    cout<<"Allowable Error: ";
    cin>>error;

    do {
        xf = f1(xi, yi, zi); yf = f2(xi, yi, zi); zf = f3(xi, yi, zi);
        cout<<count++<<' '<<xf<<' '<<yf<<' '<<zf<<endl;

        error1 = fabs(xi - xf); error2 = fabs(yi - yf); error3 = fabs(zi - zf);
        xi = xf; yi = yf; zi = zf;
    }while(error1 > error && error2 > error && error3 > error);

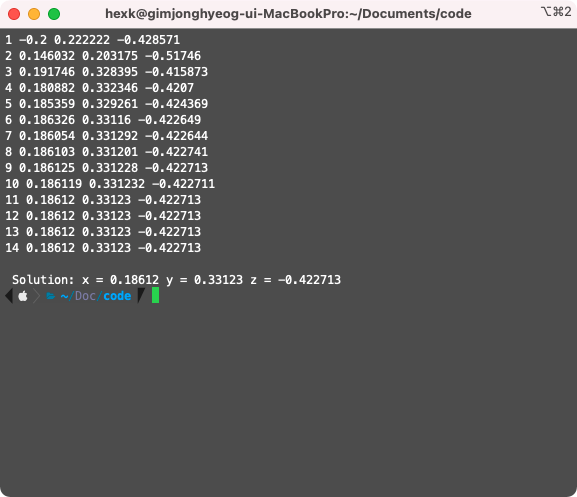
    cout<<"\n Solution: x = "<<xf<<" y = "<<yf<<" z = "<<zf<<endl;

    return 0;
}

Results

Result 1