Mathematical Sciences Labs: Detecting the L-corner on L-curve using Curvature in Backward Heat Problem

Detecting the L-corner on L-curve using Curvature in Backward Heat Problem

Backward Heat Problem 즉, Inverse Problem을 풀이하는 데 있어서 골칫거리로 작용하는 ill-posed Problem을 해결하기 위해서는 좋은(?) Regularization Parameter \(\alpha\)를 산출해야한다.

다음은 필자가 본 연구를 수행하면서 작성한 딥러닝 모델의 학습 결과이다.

Training Sets이 정확한 데이터로 이루어진 경우

Training Sets에 약간의 노이즈를 추가한 경우

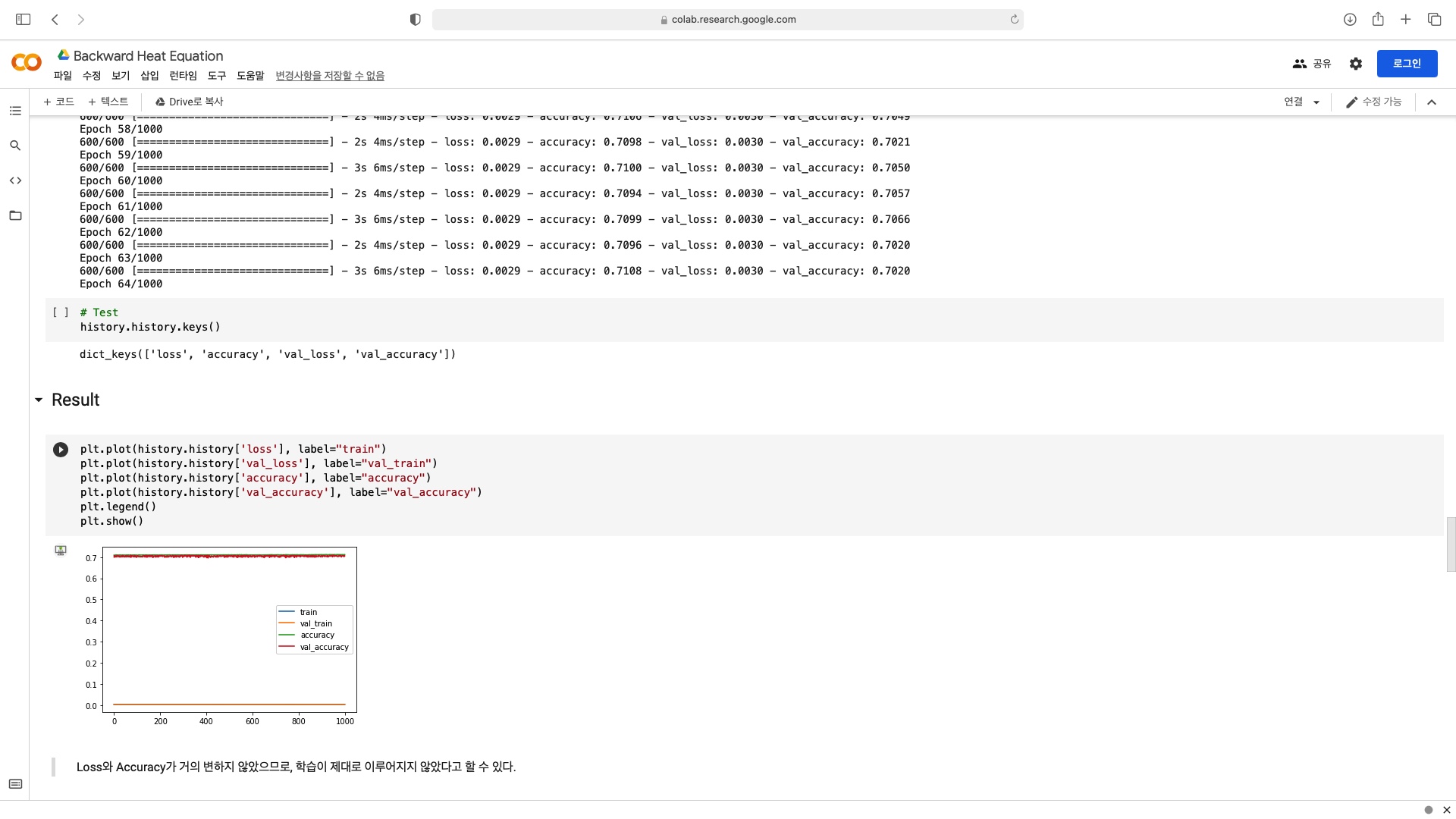
위 두 이미지를 보면, Training Sets이 정확한 데이터로 이루어진 경우에는 인공지능이 제대로 학습을 진행하고 좋은 성능을 보이지만, Training Sets에 약간의 노이즈를 추가한 경우를 보면, Loss와 Accuracy가 변하지 않고 일정한 값에서 머무르는 즉, 학습이 제대로 이루어지지 않는 상황을 확인해볼 수 있다.

이는 Inverse Problem을 풀이하는 데 있어서 약간의 입력 값의 변화 즉, 노이즈의 추가로 결과 값이 완전히 달라지는 ill-posed Problem으로 인해서 인공지능이 제대로 학습을 하지 못하는 것이다.

(어떠한 목적으로 수집되어진 실제 데이터들은 대개 이렇듯 기본적으로 노이즈가 들어있는 데이터들이므로 ill-posed되어 있다고 볼 수 있다.)

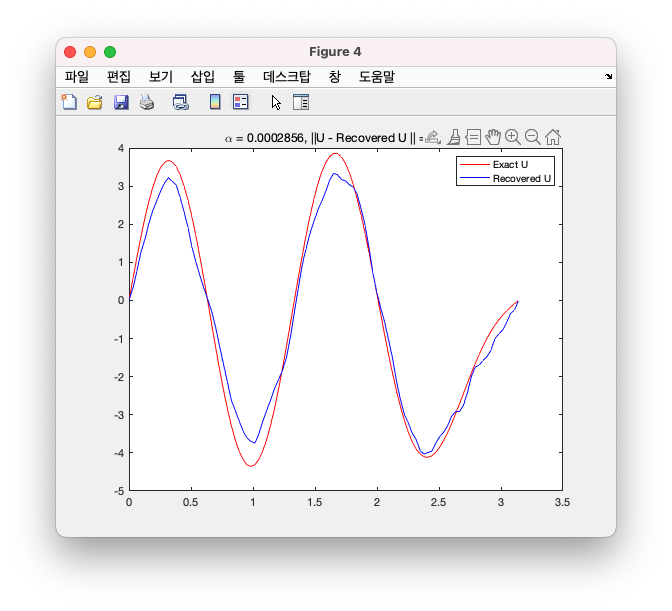
다음 이미지에서 볼 수 있듯이 우리가 구하고자 하는 빨간색 그래프를 한번에 도출해내면 좋겠지만, 위에서 설명했듯 ill-posed Problem으로 인해서 Regularization Parameter \(\alpha\)를 찾아내야 한다.

다음 그림을 보면 좋은 Regularization Parameter \(\alpha\) 값을 넣어주었을 때, 파란색 그래프(복구된 그래프)가 빨간색 그래프(정답 그래프)와 어느정도 비슷해짐을 확인할 수 있다.

그렇다면 이러한 최적의 Regularization Parameter \(\alpha\) 값을 구하기 위해서는 어떠한 방법을 사용해야할까?

더 좋은 여러 방법들이 존재하겠지만, 우선은 L-curve를 이용하여 이러한 최적의 Regularization Parameter \(\alpha\)를 찾아보도록 하겠다.

먼저 L-curve 방법으로 Regularization Parameter \(\alpha\)를 찾기 위해서는 다음과 같이 L-curve를 그리고,

그 다음 Corner에 있는 점을 찾고 그 점의 x 값을 산출해내면 그것이 최적의 Regularization Parameter \(\alpha\)가 된다.

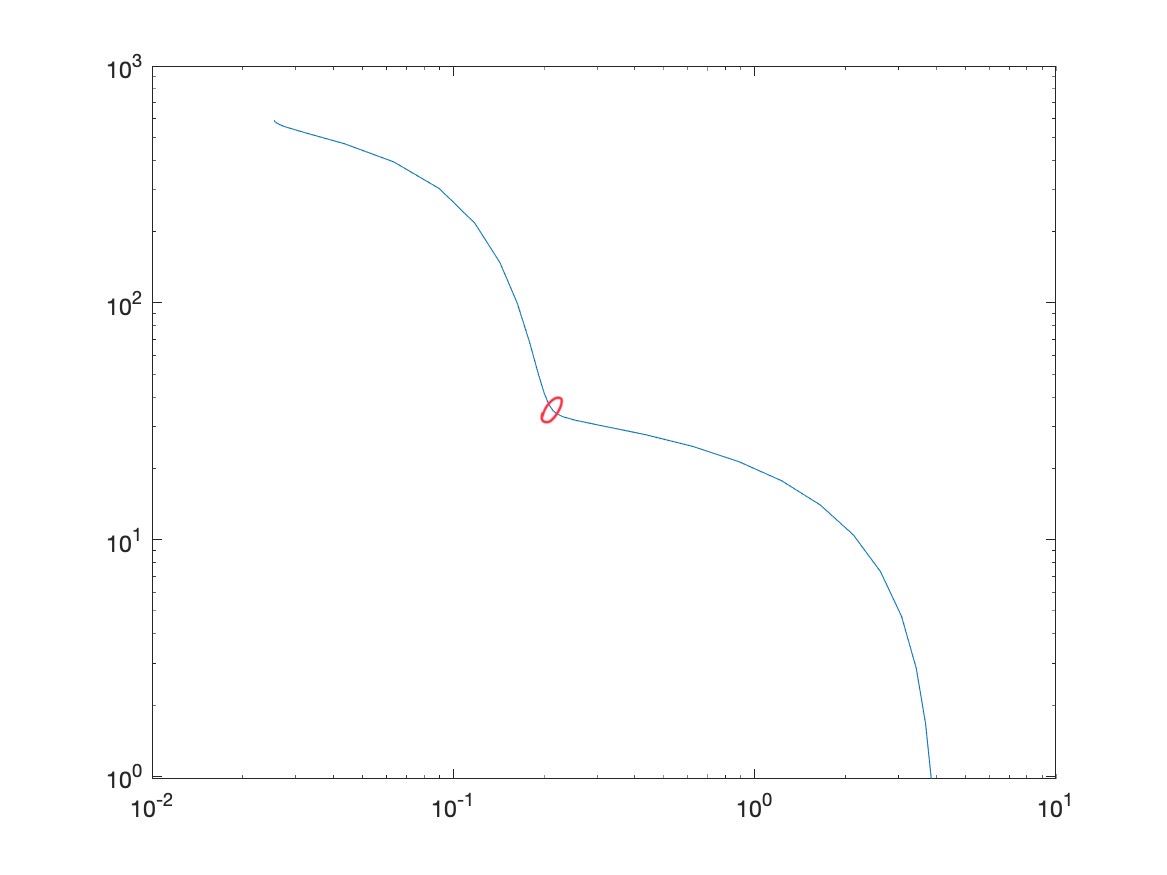
그렇다면 L-curve의 Corner를 어떻게 Detection 할 수 있을까?

이를 위해서는 먼저 다음의 Curvature 즉, 곡률의 개념을 이해해야한다.

Curvature, 곡률

Curvature란, 기하학에서 ‘굽은 정도’를 뜻하고 보통 미분적분학 과목에서 처음 마주치게 되는데, 그 때의 곡률은 기하학적 대상이 다른 공간(대체로 ‘유클리드 공간’)에 묻힌 상태에서 그 대상의 굽은 정도를 측정하는 ‘Extrinsic Curvature’ 즉, 외재적 곡률이다.

본 포스트에서는 이러한 ‘Extrinsic Curvature’(외재적 곡률)에 초점을 맞추겠다.

‘Extrinsic Curvature’(외재적 곡률)은 어떤 Plane Curve가,

Cartesian Parametric Equations \(x = x(t), y = y(t)\)로 주어진다면 다음과 같다.

\[\kappa = \frac{x'y'' - y'x''}{((x')^{2}+(y')^{2})^{3/2}}\]

또한, 우리가 흔히 알고 있는 \(y=f(x)\)의 형태로 주어진다면 다음과 같다.

\[\kappa = \frac{f''}{\{1+(f')^{2}\}^{3/2}}\]

---

증명

다음과 같이 Radius Vector \(r(t)\)로 Parametrically하게 정의되는 어떤 Plane Curve \(C\)가 있다고 해보자.

Curve 위의 각 점 \(M\)과 \(M_{1}\)에서 접선을 그었을 때, 그 회전각을 \(\Delta{\phi}\)라고 하면,

이러한 회전각 \(\Delta{\phi}\)는 곡선 위에서 점이 이동하는 거리에 따라서 변화하기 때문에 다음과 같이 식을 작성할 수 있다.

\[\frac{\Delta{\phi}}{\Delta{s}}\]

이것이 평균 곡률의 개념이다.

즉, 평균 곡률의 식은 다음과 같다.

\[Average \text{ } \kappa = \frac{\Delta{\phi}}{\Delta{s}}\]

여기서 \(lim_{\Delta{s} \to 0}\)을 취하면 작은 구간에서의 곡률을 산정할 수 있다.

\[\kappa = \lim_{\Delta{s} \to 0}{\frac{\Delta{\phi}}{\Delta{s}}} = \frac{d{\phi}}{d{s}}\]

위의 곡률 식 우변의 분모, 분자를 미소 시간 변화량 \(d{t}\)로 나눠주면 다음과 같고,

\[\kappa = \frac{\frac{d{\phi}}{d{t}}}{\frac{d{s}}{d{t}}}\]

여기서 \(d{s}\)는 \(Pythagoras's\text{ }theorem\)에 의해 \(\sqrt{(d{x})^{2} + (d{y})^{2}}\)이다.

즉,

\[d{s} = \sqrt{(d{x})^{2} + (d{y})^{2}}\]

왜냐하면, 곡선 \(\Delta{s} \to 0\)이면 이를 직선으로 바라볼 수 있기 때문이다.

이를 다시 위의 곡률 식에 대입하여 정리하면,

\[\kappa = \frac{\frac{d{\phi}}{d{t}}}{\frac{d{s}}{d{t}}} = \frac{\frac{d{\phi}}{d{t}}}{\frac{\sqrt{(d{x})^{2} + (d{y})^{2}}}{d{t}}} = \frac{\frac{d{\phi}}{d{t}}}{\sqrt{(\frac{d{x}}{d{t}})^{2}+{(\frac{d{y}}{d{t}})^{2}}}}\]

시간 \(t\)에 대한 미분으로 바라볼 수 있으므로 한번 더 식을 정리하면,

\[\kappa = \frac{\frac{d{\phi}}{d{t}}}{\sqrt{(\frac{d{x}}{d{t}})^{2}+{(\frac{d{y}}{d{t}})^{2}}}} = \frac{\frac{d{\phi}}{d{t}}}{\sqrt{(x')^{2}+(y')^{2}}}\]

여기서 \(\frac{d{\phi}}{d{t}}\)는 다음 식으로부터 유도할 수 있는데,

\[tan(\phi) = \frac{d{y}}{d{x}}\]

위 식의 우변의 분모, 분자를 미소 시간 변화량 \(d{t}\)로 나눠주면, 이는 시간에 대한 미분으로 볼 수 있으므로,

\[tan(\phi) = \frac{d{y}}{d{x}} = \frac{\frac{d{y}}{d{t}}}{\frac{d{x}}{d{t}}} = \frac{y'}{x'}\]

양변을 t에 대해서 미분하면,

\[\frac{d}{d{t}}{tan(\phi)} = (\frac{y'}{x'})'\]

• 우변을 t에 대해서 미분하면,

\[\frac{d}{d{t}}{tan(\phi)} = (\frac{y'}{x'})' = \frac{y''x' - x''y'}{(x')^{2}}\]

• 좌변을 t에 대해서 미분하면,

\[sec^{2}{\phi}\frac{d{\phi}}{d{t}} = (\frac{y'}{x'})'\]

위 미분의 결과를 정리하면 다음과 같고,

\[sec^{2}(\phi)\frac{d{\phi}}{d{t}} = \frac{y''x' - x''y'}{(x')^{2}}\]

그러므로 \(\frac{d{\phi}}{d{t}}\)는 다음과 같다.

\[\frac{d{\phi}}{d{t}} = \frac{1}{sec^{2}(\phi)}\cdot\frac{y''x' - x''y'}{(x')^{2}}\]

여기서 \(sec^{2}(\phi)\)는 삼각함수의 공식에 의해서 \(1 + tan^{2}(\phi)\)이므로 즉,

\[sec^{2}(\phi) = 1 + tan^{2}(\phi)\]

이를 위의 식에 대입하면,

\[\frac{d{\phi}}{d{t}} = \frac{1}{sec^{2}(\phi)}\cdot\frac{y''x' - x''y'}{(x')^{2}} = \frac{1}{1 + tan^{2}(\phi)}\cdot\frac{y''x' - x''y'}{(x')^{2}}\]

또한, \(tan(\phi)\)는 위에서 \(\frac{y'}{x'}\)이므로 이를 이용하여 식을 정리하면 다음과 같다.

\[\frac{d{\phi}}{d{t}} = \frac{1}{1 + (\frac{y'}{x'})^{2}}\cdot\frac{y''x' - x''y'}{(x')^{2}} = \frac{y''x' - x''y'}{(x')^{2} + (y')^{2}}\]

그러므로 위의 \(\frac{d{\phi}}{d{t}}\)의 식을 다음 식에 대입하고,

\[\kappa = \frac{\frac{d{\phi}}{d{t}}}{\sqrt{(x')^{2}+(y')^{2}}}\]

정리하면 최종 식은 다음과 같다.

\[\kappa = \frac{\frac{y''x' - x''y'}{(x')^{2} + (y')^{2}}}{\sqrt{(x')^{2} + (y')^{2}}} = \frac{y''x' - x''y'}{\{(x')^{2} + (y')^{2}\}^{3/2}}\]

다음은 필자가 수기로 작성한 위의 Curvature에 대한 증명이다.

---

위에서 어떤 Plane Curve \(C\)가 y=f(x)로 정의된다면, 곡률 \(\kappa\)는 다음과 같다.

\[\kappa = \frac{f''}{\{1 + (f')^{2}\}^{3/2}}\] \[(\because{y' = f', y'' = f'', x' = 1, x'' = 0})\]

Applications of Curvature - Detecting the L-corner

위에서 곡률 Curvature에 대해서 알아보았다.

이제 이것을 L-curve의 L-corner를 도출한다는 관점에서 바라보자.

위에서 곡률 Curvature는 ‘굽은 정도’를 뜻한다고 했기 때문에, L-curve에서 최대로 많이 굽은 부분이 결국엔 L-curve의 L-corner가 됨을 직관적으로 생각해볼 수 있다.

교수님께서 L-curve를 Draw하시기 위해서 작성하신 다음의 코드를 보면,

loglog(xx,yy)

\(y=f(x)\)로 정의되는 곡률 \(\kappa\) 식을 적용할 수 있으므로, 필자는 Matlab에서 다음과 같은 코드를 작성하여,

spl = spline(xx,yy);

fp = fnder(spl);
fpp = fnder(spl,2);
K = @(x) fnval(fpp,x)./(1 + fnval(fp,x).^2).^(3/2);

figure
ezplot(K,[min(x),max(x)]);
axis([min(x),max(x)/2,-1e-1,1.5e-1]);

다음과 같이 L-curve에 대한 Curvature를 Draw할 수 있었으며,

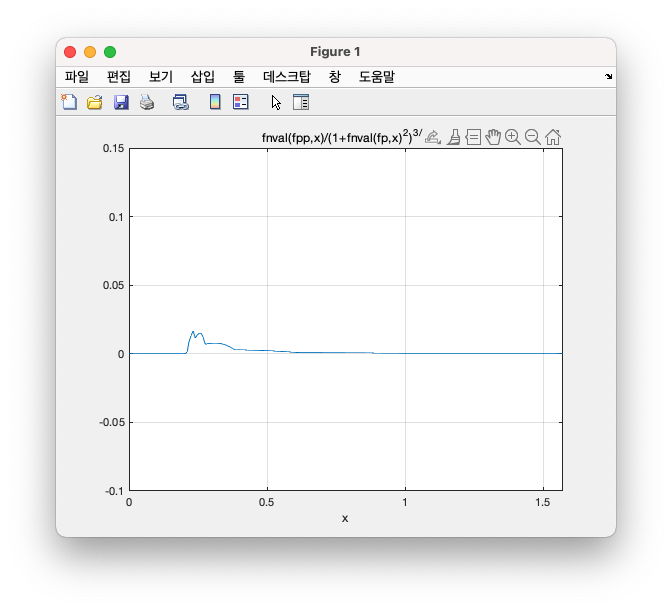
또한, 다음과 같이 L-curve의 Curvature에서의 y의 최댓값을 산출하여 그 값으로부터 x 즉, 최적의 Regularization Parameter \(\alpha\) 값을 도출해낼 수 있었다.

j = 0;

for i = 1:100
    j(i) = K(x(i));
end

TF = islocalmax(j, 'MinProminence', 5.0e-3);

alpha = x(TF)
alpha = alpha*10^(-3)

최종적으로, 그 \(\alpha\) 값에 대한 Curve는 다음과 같았다.

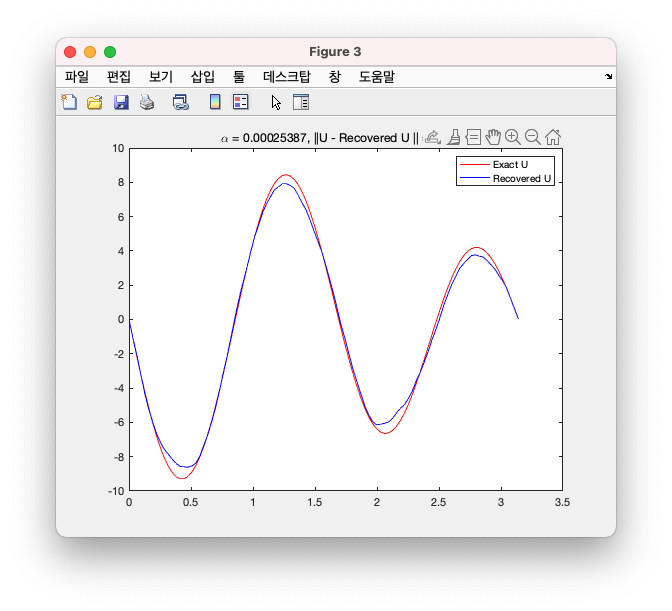
Questions

이렇게 연구를 진행하면서 다음과 같은 궁금증이 생겼다.

컴퓨터 자원이 한정적임에 따라 xx와 yy의 개수를 늘려서 좋은 Regularization Parameter \(\alpha\)의 근사치를 찾아낸다고 하더라도 소수점 이하 몇 자리 수에서 달라진다면, 데이터의 민감성으로 인해 파란색 그래프(복구된 그래프)가 빨간색 그래프(정답 그래프)에 fit하지 못하는 이러한 근본적인 문제는 어떻게 해결할 수 있을까?

이에 대해 교수님께 개인적으로 질문드린 결과, 교수님께서는 지금과 같이 흔히 알려진 Backward Heat Equation의 경우에는 이상적인 L-curve가 도출됨에 따라 필자의 방법이 통용될 수 있으나, 일반적인 상황에서는 대개 이러한 최적의 Regularization Parameter \(\alpha\) 값을 도출하기 위해서는 추가로 필요한 여러 연산들이 있다고 말씀해주셨다.

Forward Plans

• 다른 예제들에서도 본 포스팅의 방법을 이용하여 Optimal Solution에 가까운지 확인해본다.

• 만약 이상이 없다면, 데이터를 생성하여 Training 해본다.