Geomatics Engineering: 거리오차 증명

질문

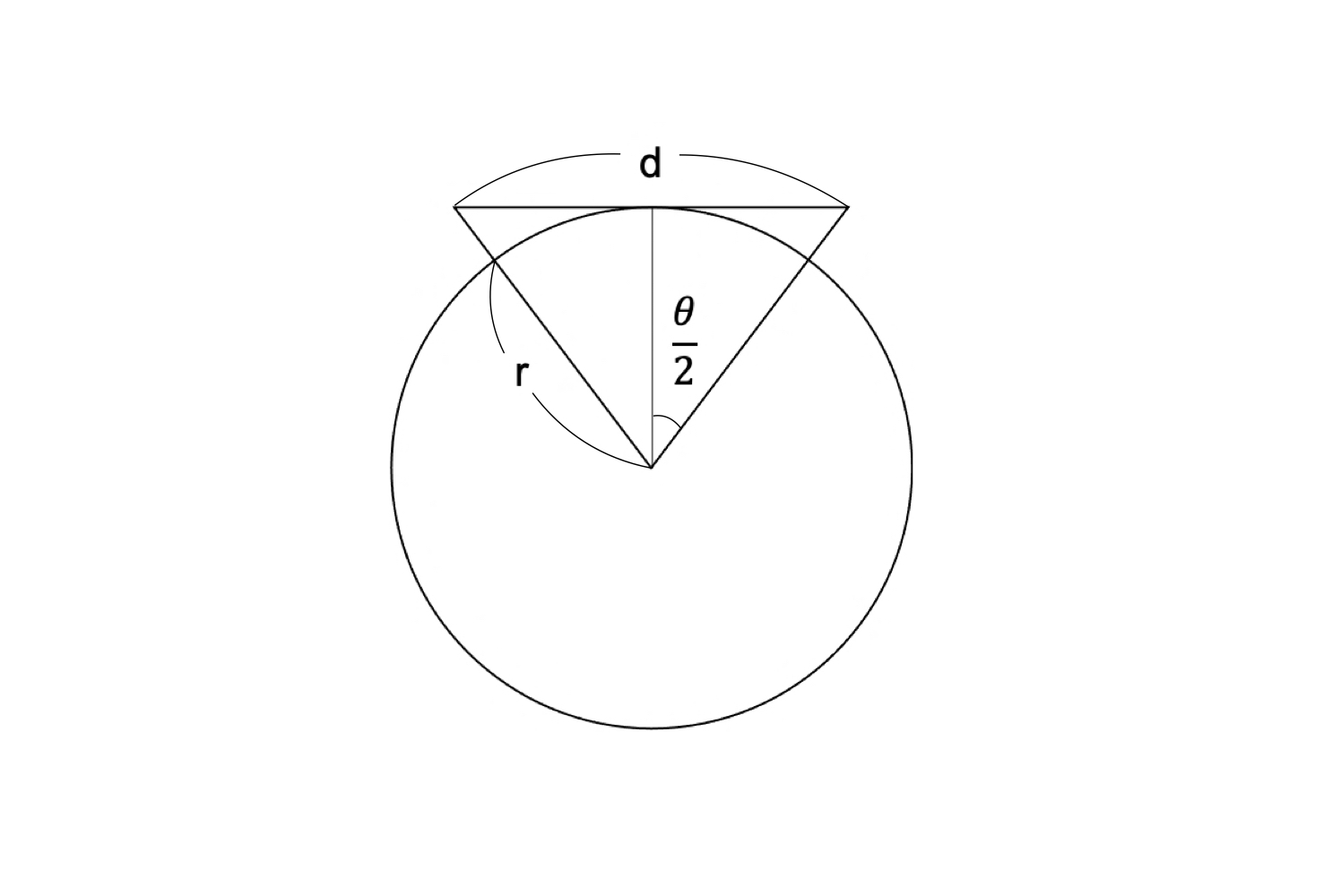
다음 거리오차를 증명하라.

\[d-D = \frac{D^{3}}{12r^{2}}\] \[(\text{Here, } D = 2r\frac{\theta}{2})\]

답변

\[\tan{\frac{\theta}{2}} = \frac{\frac{d}{2}}{r}\] \[\therefore d = 2r\tan{\frac{\theta}{2}}\]

\[\text{Here,}\] \[\text{By Taylor series}\] \[tan{\frac{\theta}{2}} = \frac{\theta}{2} + \frac{1}{3}(\frac{\theta}{2})^{3} + \cdots\] \[\therefore d = 2r\{\frac{\theta}{2} + \frac{1}{3}(\frac{\theta}{2})^{3}\}\]

\[d = 2r\{\frac{\theta}{2} + \frac{1}{3}(\frac{\theta}{2})^{3}\} = 2r\{\frac{D}{2r} + \frac{1}{3}(\frac{D}{2r})^{3}\}\] \[(\because \frac{\theta}{2} = \frac{D}{2r})\] \[= D + \frac{2r}{3}(\frac{D^{3}}{8r^{3}})\] \[= D + \frac{D^{3}}{12r^{2}}\]

\[\therefore d-D = \frac{D^{3}}{12r^{2}}\]