Mechanics of Materials: Tensile Strength Test - 2

June 21, 2021 4 분 소요

Tensile Strength Test

지난 편에 이어서 재료역학 시간에 실시한 인장 시험 보고서의 내용을 공개하고자 한다.

먼저 탄성계수부터 살펴보자.

탄성계수

탄성계수란 재료의 강성도(stiffness)를 나타내는 값으로서 공칭 응력-변형율 선도의 선형 구간에서의 기울기이다.

이전 시간에 우리는 SM.csv 파일로부터 데이터를 불러들여 공칭 응력-변형율 선도를 python을 통해 draw 해보았다.

이번에는 탄성계수를 도출하기 위해서 공칭 응력-변형율 선도로부터 선형 구간을 찾아내고 그 선형 구간에서의 데이터를 기반으로 기울기 값 즉, 탄성계수를 도출해보자.

먼저 공칭 응력-변형율 선도에서 선형 구간을 찾기 위해서 필자는 다음의 생각을 떠올렸다.

양수이면서 가장 앞서는 기울기 데이터를 기준으로 설정하여 그 이후에 등장하는 기울기 값과의 차이가 설정한 범위 내에 존재한다면 그 값이 선형 구간에서의 기울기이다.

말이 이해가 가지 않을 수 있으니 직접 코드로 보이면서 이를 설명하겠다.

먼저 지난 편에서 작성한 전체 코드를 가져오자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

위 코드에서 먼저 기울기 데이터를 담을 리스트를 하나 선언하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
slope_l = []        # 기울기 데이터를 담을 리스트

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

이제 기울기 값을 도출해내야 하는데 이는 다음의 식으로부터 도출해낼 수 있다.

\[slope = \frac{\Delta{Strain}}{\Delta{Stress}}\]

또한, 이미 stress와 strain 데이터를 각각 stress, strain 리스트에 삽입했으므로 이를 이용하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
slope_l = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

for i in range(0, len(stress)-1):
    slope = (strain[i+1] - strain[i]) / (stress[i+1] - stress[i])

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

그런데 필자가 위의 아이디어에서 말했듯 양수 기울기가 필요하므로 반복문 내에 조건(기울기 값이 양수)을 걸고 그 조건을 만족할 때에 기울기 값을 리스트에 삽입하는 동작을 수행하게끔 하자.

또한, 몇 번째 데이터로부터 해당 기울기 값을 도출해내었는지 확인하기 위해 반복문에 의해 카운트 되는 변수(아래 코드에서 i)의 값도 리스트에 삽입하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
slope_l = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

for i in range(0, len(stress)-1):           # Index Error를 미연에 방지하기 위해 stress의 길이에서 1을 뺌
    slope = (strain[i+1] - strain[i]) / (stress[i+1] - stress[i])       # 위에서 기울기를 도출해내기 위해 작성한 수식에 의해

    if(slope > 0):      # 기울기 값이 0보다 크면
        slope_l.append([i, slope])          # slope_l 리스트에 i 값과 기울기 값을 리스트로 묶어서 삽입

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

그 후 기울기를 삽입한 slope_l 리스트를 순회하면서 첫 번째 기울기가 첫 번째 이후의 기울기와 그 차이가 0.0000005 이내일 때에만 slope_l의 원소를 출력하도록 하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
slope_l = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

for i in range(0, len(stress)-1):
    slope = (strain[i+1] - strain[i]) / (stress[i+1] - stress[i])

    if(slope > 0):
        slope_l.append([i, slope])

for i in range(1, len(slope_l)):        # 첫 번째 이후의 slope_l 원소에 접근하기 위함
    if(abs(slope_l[0][1] - slope_l[i][1]) < 0.0000005):         # 첫 번째 기울기가 첫 번째 이후의 기울기와 그 차이가 0.0000005 이내일 때
        print(slope_l[i])         # slope_l 리스트의 원소 출력

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

출력의 결과가 다음과 같다면 성공이다.

위 출력 결과를 분석해보면 343번째 데이터 이후에 갑자기 1418번째 데이터가 등장함을 확인할 수 있는데, 이는 다음의 공칭 응력-변형율 선도를 확인해보면 어느정도 유추를 해볼 수 있다.

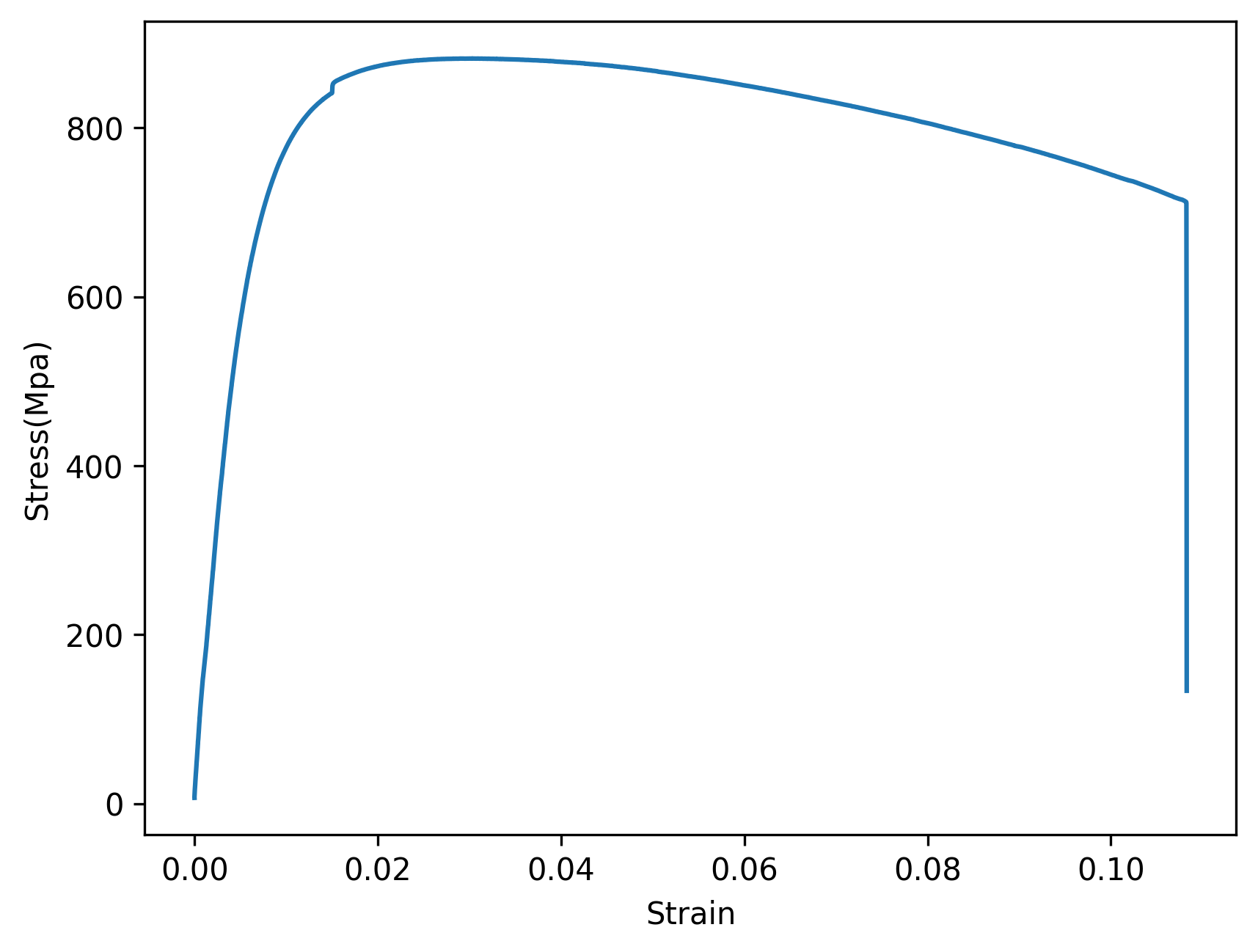
즉, 양수이면서 가장 앞선 기울기 데이터와 차이가 0.0000005 이내인 기울기가 다음의 공칭 응력-변형율 선도에서

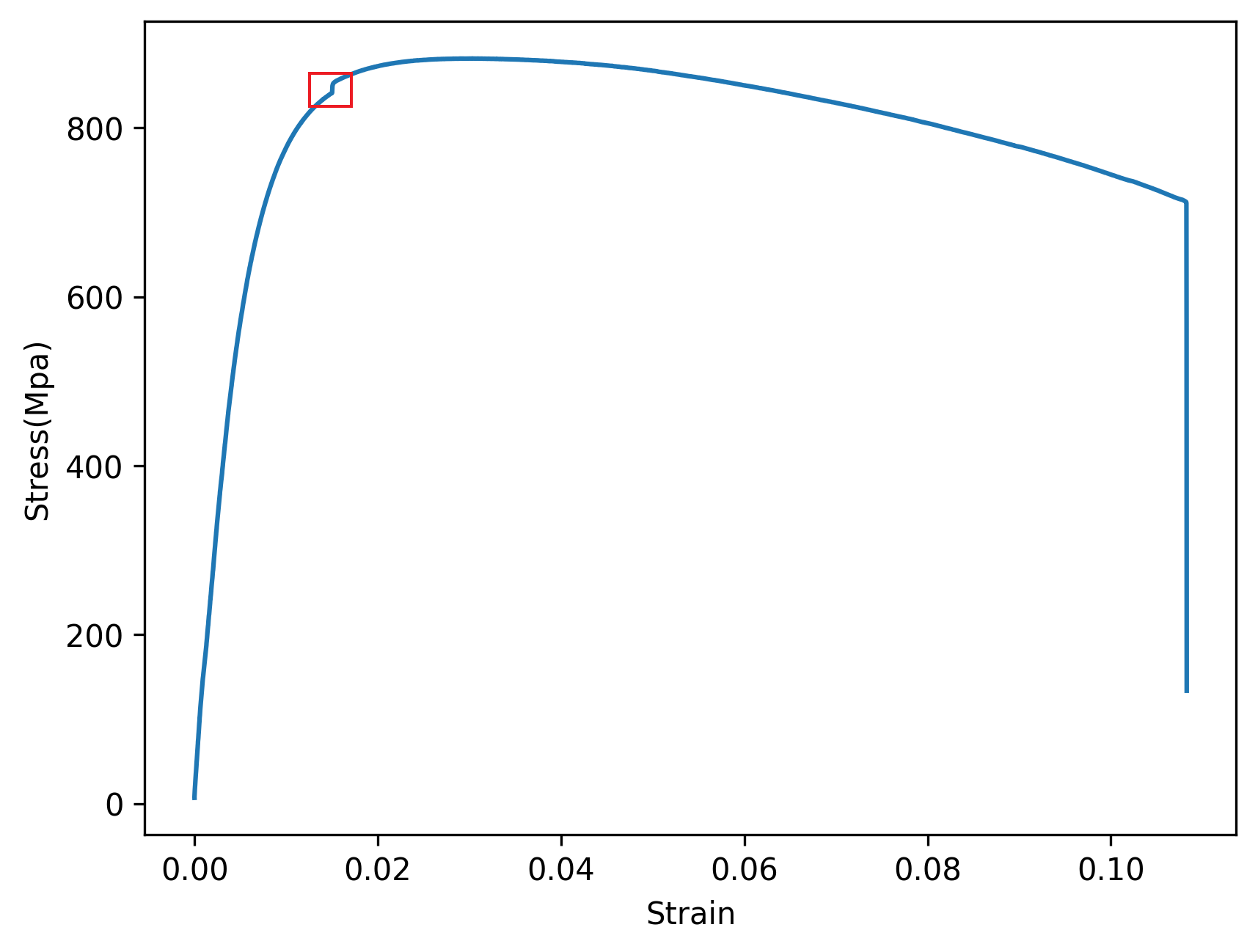
대략 위의 빨간색 네모친 부분에 위치함을 유추해볼 수 있다.

그러므로 우리는 가장 앞에서부터 300~350개의 데이터만을 가지고 이 데이터들을 가장 잘 대표하는 기울기를 하나 찾아낸다면 그것이 곧 탄성계수가 됨을 생각해볼 수 있다.

먼저 위에서 작성했던 전체 코드 중

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
slope_l = []      # 기울기 관련 코드

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)


# 기울기 관련 코드
for i in range(0, len(stress)-1):
    slope = (strain[i+1] - strain[i]) / (stress[i+1] - stress[i])

    if(slope > 0):
        slope_l.append([i, slope])

# 기울기 관련 코드 
for i in range(1, len(slope_l)):
    if(abs(slope_l[0][1] - slope_l[i][1]) < 0.0000005):
        print(slope_l[i])

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

선형 구간을 찾아내기 위해 삽입했던 기울기 관련 구문들을 모두 삭제하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

이제 stress_ex, strain_ex 리스트를 선언하여 350개의 stress와 strain 데이터들을 저장하자.

이때도 역시 기존의 stress와 strain 리스트를 활용하자.

import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
stress_ex = []
strain_ex = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

for i in range(0, 350):
    stress_ex.append(stress[i])
    strain_ex.append(strain[i])

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

그 후 350개의 stress와 strain을 가장 잘 대표하는 기울기를 찾고 이를 출력해보자.

이를 위해 우리가 직접 알고리즘을 구현할 필요는 없다.

numpy에서 제공하는 polyfit이라는 함수를 이용하면 된다.

import numpy as np
import matplotlib.pyplot as plt
import csv

sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
stress_ex = []
strain_ex = []

next(rdr); next(rdr)

for line in rdr:
    stress.append(float(line[8])); strain.append(float(line[9])/100)

for i in range(0, 350):
    stress_ex.append(stress[i])
    strain_ex.append(strain[i])

slope_intercept = np.polyfit(strain_ex, stress_ex, 1)       # strain_ex, stress_ex 리스트의 원소들(strain, stress의 350개의 데이터들)을 가장 잘 대표하는 기울기와 y 절편 산출

print(slope_intercept)

plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")

plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")

sm.close()

위 코드의 실행 결과가 다음과 같이 도출되었다면 성공이다.

[1.25515487e+05 2.43356112e+01]

왜 결과 값이 하나가 아닌 두 개가 도출되었는지 의문이 생길 수 있다. (위 코드에서 주석을 먼저 확인해본 사람이라면 그 답을 알 수 있다.)

polyfit 함수는 기울기 값 뿐만 아니라 직선의 y 절편 값도 반환하기 때문이다.

즉, 우리가 구하고자 하는 값은 2.43356112e+01이다. (이것이 탄성계수 값이다.)

탄성계수 값 도출을 마지막으로 이번 편을 마무리 짓고 다음 편에서는 보고서에 작성한 0.2% 오프셋 방법을 설명하도록 하겠다.

Twitter Facebook LinkedIn

Jonghyeok Kim

Mechanics of Materials: Tensile Strength Test - 2

Tensile Strength Test

탄성계수

공유하기

댓글남기기

참고

Capstone Design: 종합설계보고서 및 요약보고서

Notice: 2023년 10월 30일(월) Audio Player 탑재

Exhibition: The Tom Project

Plans: 23.04.23