Mechanics of Materials: Tensile Strength Test - 1
Tensile Strength Test
내용
5월 25일부터 진행되었던 재료역학 실험실습 보고서 작성 과제가 어제 잘 마무리가 되었고, 본 포스팅을 통해 필자가 그 결과를 보이고자 한다.
먼저 실험실습은 코로나 상황으로 인해서 온라인으로 진행되었기 때문에 단순 영상시청으로만 실험 과정을 확인해볼 수 있었으며, 다음과 같이 인장시험의 결과 도출된 데이터만 csv 파일로 주어졌다.
인장시험에 사용된 시험편은 국민 강재로 알려진 SM45C이다. 이것에 대해서 간략히 설명을 하자면, SM45C는 기계구조용 탄소강재로서, 열처리나 경화 작업을 통해 기계적 강도가 요구되는 부품의 재료로 사용되고 있다. 일반적으로 SM재에서 많이 사용하는 재질은 지금 다루고 있는 SM45C와 SM35C를 주로 많이 사용한다. 또한, SM45C에서 S와 M은 Steel과 Machine의 앞 글자를 딴 것이고, 45는 탄소함유량을 나타내며, C는 탄소를 의미한다. 마지막으로 국민 강재로 불리게 된 이유도 설명을 하자면, 철과 탄소가 아주 흔한 물질이고, 화학적 결합이 쉬워서이며, 가공성과 강도가 괜찮기 때문이다.
이 정도로 간략히 설명을 마치고, 위에서 주어진 csv 데이터들을 이용해서 본 보고서가 요구한 사항들을 해결해보기로 하겠다. 먼저 보고서의 요구사항을 확인해보자.
- 공칭 응력-변형율 선도
- 탄성계수
- 0.2% 오프셋에 의한 항복응력
- 극한강도
- 파단연신율
csv 파일의 데이터들을 Excel을 통해서 처리해도 되지만, 필자는 한 걸음 더 나아가 Python을 이용해보았다.
csv 파일의 데이터를 처리하기 위해서는 다음과 같이 Python에서 csv 파일을 열고 그 데이터를 읽어들여야 한다.
import csv
sm = open("SM.csv", "r")
rdr = csv.reader(sm)
sm.close()
데이터를 읽어들인 후에는 다음과 같이 반복문을 통해서 행 단위로 데이터를 읽어들일 수 있다.
for line in rdr:
# Ex. line[0] line[1] line[2] ...
공칭 응력-변형율 선도
공칭 응력-변형율 선도를 그리기 위해서는 변형율(Strain) 값과 응력(Stress) 값이 필요한데, csv 파일에서 이미 Stress data를 Mpa 단위로 제공해주고 있기 때문에 문제 될 것이 없으나, Strain의 경우에는 표면적으로 그 data가 드러나 있지 않기 때문에 어떤 data를 통해서 Strain의 값을 도출해내야 한다.
csv file을 잘 살펴보면, Elongation Percent data가 존재하고, 해당 data는 다음의 식으로부터 유도되었으며,
\[Elongation = \frac{\Delta{L}}{L}\times{100}(\%)\]위 식에서 \(Strain = \varepsilon = \frac{\Delta{L}}{L}\) 이므로, Elongation Percent data를 단순히 100으로 나눠주기만 하면 그 값이 Strain이라는 것은 자명하다.
그러므로 다음과 같이 코드를 작성하여 Stress data(9 Column)는 Stress List에, Strain data는 Elongation Percent data(10 Column)를 100으로 나누어 Strain List에 삽입하자.
물론 데이터 처리시에 기본적으로 읽어들인 값의 type은 str이므로, 형 변환을 해주어야 함을 잊지 말자.
import csv
sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
for line in rdr:
stress.append(float(line[8])); strain.append(float(line[9])/100)
sm.close()
그런데 1, 2 row는 수치가 아닌 category와 unit data이므로 3 row부터 읽어들여야 한다.
그러므로 다음과 같이 코드를 작성하자.
import csv
sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
next(rdr); next(rdr)
for line in rdr:
stress.append(float(line[8])); strain.append(float(line[9])/100)
sm.close()
위 코드를 작성한 후 다음의 print문을 추가하여 stress와 strain이 각 List에 잘 삽입되었는지 확인해보자.
print(stress); print(strain)
코드의 실행결과가 Error 없이 다음과 같이 도출되었다면, 성공이다.
이제 읽어들인 Strain과 Stress 데이터를 가지고, matplotlib 라이브러리를 이용해서 Graph를 그려볼 것이다.
다음과 같이 코드를 작성하자.
import matplotlib.pyplot as plt
import csv
sm = open("SM.csv", "r")
rdr = csv.reader(sm)
stress = []
strain = []
next(rdr); next(rdr)
for line in rdr:
stress.append(float(line[8])); strain.append(float(line[9])/100)
plt.plot(strain, stress)
plt.xlabel("Strain"); plt.ylabel("Stress(Mpa)")
plt.savefig("S-S Curve.png", dpi=300, bbox_inches="tight")
sm.close()
위 코드를 실행한 후, 코드 파일과 동일한 Path에 다음과 같이 S-S Curve.png 파일이 생성되고,
그 결과, 다음과 같은 그래프가 도출되었다면 성공이다.
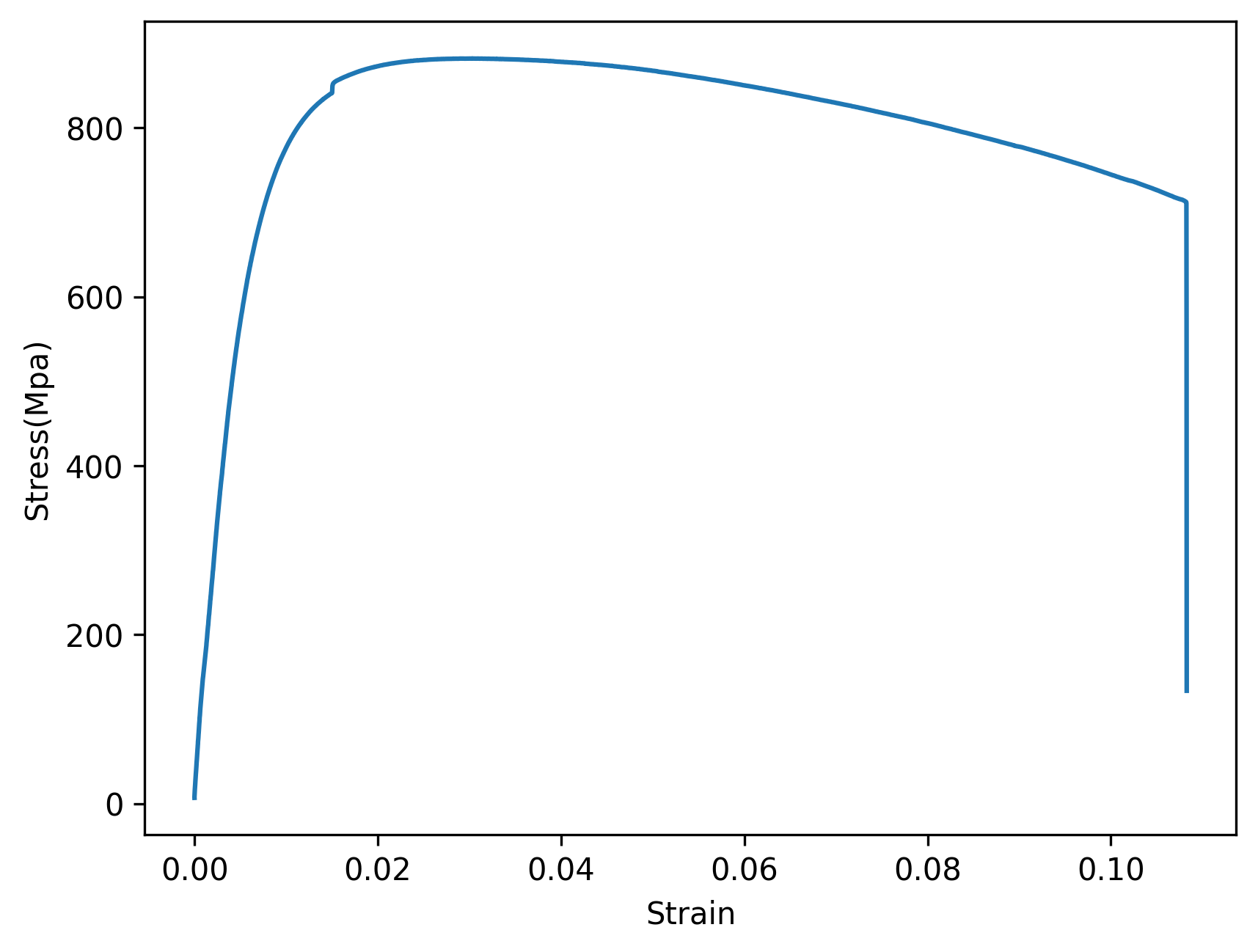
위 코드에서 plot에 인자를 보낼 때 먼저 보낸 Data가 x, 뒤에 보낸 Data가 y가 된다는 사실을 유념하자. 또한, 필자는 가로축과 세로축에 각각 Strain, Stress(Mpa)를 레이블로 설정하였는데, Strain은 무차원이기 때문에 Stress에서처럼 따로 단위를 기재하지는 않았다.
그렇게 도출된 Graph를 show()해도 되나, 보고서 특성상 따로 이미지를 첨부해야 하기 때문에 필자의 경우에는 savefig()를 했다.
여기서 1편을 마무리 짓고, 다음 편에서는 탄성계수를 도출해낸 과정과 0.2% 오프셋 방법을 이용하여 항복응력을 도출해낸 과정을 설명하겠다.

댓글남기기