Relative Error of Closure

Relative Error of Closure

내용

결합 트래버스에서 폐합비를 도출해내었을 때, 폐합비가 허용범위 내에 들어오지 않을 경우 재측의 상황에 놓이게 된다.

이러한 경우 임의로 측선을 조정하고 다시 폐합비를 계산하여 이를 확인하는 과정이 필요한데, 어떠한 의미도 포함하지 않은 단순 계산이므로 컴퓨터에게 이러한 작업을 맡겨보기로 했다.

아래는 이번 측량학 조별 과제를 수행하면서 내가 작성한 파이썬 프로그램이다.

코드

import math
import random

bef_d = [[359, 31, 31.67], [271, 33, 18.34], [231, 37, 5.01], [214, 30, 51.68], [181, 12, 13.34], [90, 0, 0.01]]; 
aft_d = []; leng = [45.56, 24.93, 11.03, 18.91, 23.35, 45.52]; aft_leng = [0, 0, 0, 0, 0, 0]; n = []; e = []; flag = 0

def dms2deg(bef_d):
    return bef_d[0]+bef_d[1]/60+bef_d[2]/3600

while(True):
    deg = []; n_t = 0; e_t = 0; d = 0

    if(flag == 0):
        for i in range(0, 6):
            aft_d.append(dms2deg(bef_d[i])); n.append(round(leng[i]*math.cos(math.radians(aft_d[i])), 3)); n_t += n[i]; e.append(round(leng[i]*math.sin(math.radians(aft_d[i])), 3))
            e_t += e[i]

        err = round(math.sqrt(math.pow(n_t, 2)+math.pow(e_t, 2)), 3)

        for i in leng: d += i

        r = err/d

        print(aft_d); print(n); print(e); print(round(n_t, 3)); print(round(e_t, 3)); print(err); print(r)

        if(r < 1/3000):
            print("허용오차 범위 내 존재"); break
        else:
            print("허용오차 범위 내 존재하지 않음"); all = random.randrange(1, 5); flag = 1

    else:
        for i in range(0, 6):
            aft_leng[i] = random.randrange(int(math.modf(leng[i])[1])-all, int(math.modf(leng[i])[1])+all+1) + float(math.modf(leng[i])[0])
            n[i] = round(aft_leng[i]*math.cos(math.radians(aft_d[i])), 3); n_t += n[i]
            e[i] = round(aft_leng[i]*math.sin(math.radians(aft_d[i])), 3); e_t += e[i]

        err = round(math.sqrt(math.pow(n_t, 2)+math.pow(e_t, 2)), 3)

        for i in aft_leng: d += i

        r = err/d

        print(aft_d); print(n); print(e); print(round(n_t, 3)); print(round(e_t, 3)); print(err); print(r); print(aft_leng); print(d)

        if(r < 1/3000):
            print("허용오차 범위 내 존재"); print(aft_leng); break
        else:
            print("허용오차 범위 내 존재하지 않음"); all = random.randrange(1, 5); flag = 1

코드 설명

1~4 범위 내에서 하나의 값을 랜덤으로 도출하게끔 하고 그 값을 이용하여 기존의 재측 이전의 측선 거리의 반경값을 계산하였으며, 이러한 반경 내에서 랜덤하게 거리를 도출해내었다.

뿐만 아니라, 도출된 거리 값을 이용하여 폐합비를 계산하였으며, 그 폐합비가 \(\frac{1}{3000}\)보다 작은 경우에만 그때의 조정된 측선의 거리 값을 출력하게 했다.

물론 여기서 반경 내의 값이 소수점 이하의 값이 존재하지 않는 즉, 기존 측선 거리 값에 비해 정밀도가 떨어지는 값이 아니냐고 반문할 수 있어서, 필자는 먼저 기존 측선의 거리 값에서 정수부와 실수부로 분리하여 정수부 기준으로 반경 1~4까지의 랜덤 값을 뽑아내고 그 값에 분리해놓은 실수부를 결합시키는 방식으로 소수점 이하의 값이 손실되는 것을 방지하였다.

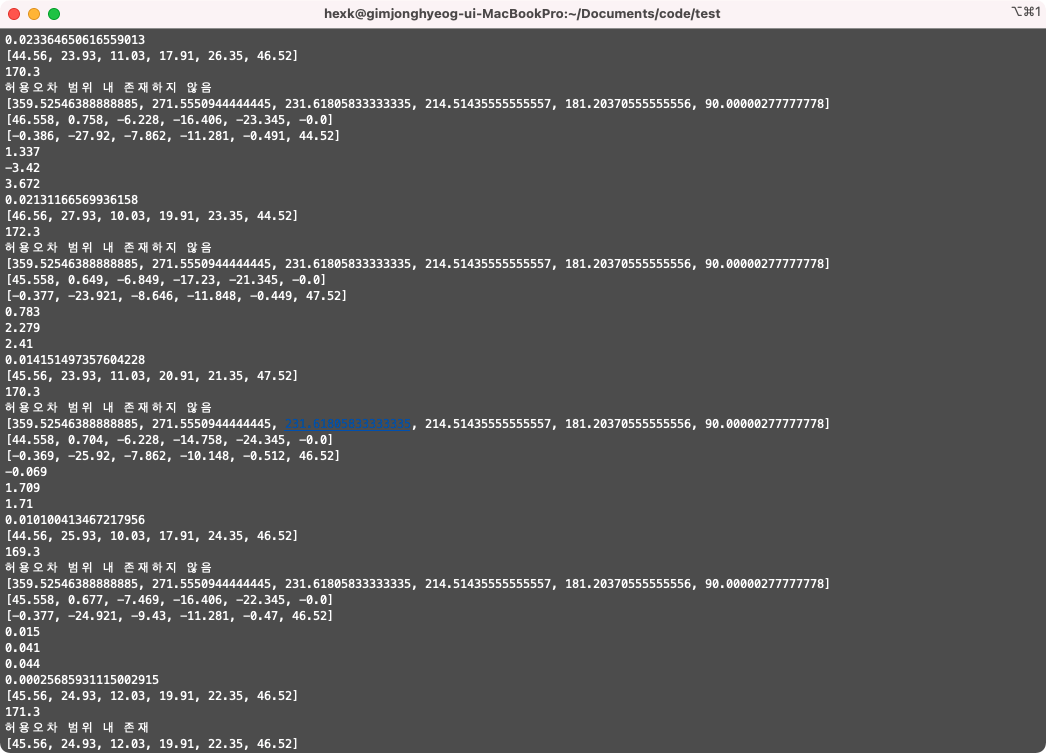
위 프로그램을 실행한 결과는 아래와 같다.

실행 결과