Calculus: Functions and Limits - Calculating Limits Using the Limit Laws

Question

Question 1

(a) What is wrong with the following equation?

\[\frac{x^{2}+x-6}{x-2} = x + 3\]

(b) In view of part (a), explain why the equation

\[\lim_{x\to{2}}\frac{x^{2} + x - 6}{x - 2} = \lim_{x\to{2}}(x + 3)\]

is correct.

Question 2

Is there a number \(a\) such that

\[\lim_{x\to{-2}}{\frac{3x^{2}+ax+a+3}{x^{2}+x-2}}\]

exists? If so, find the value of \(a\) and the value of the limit.

Question 3

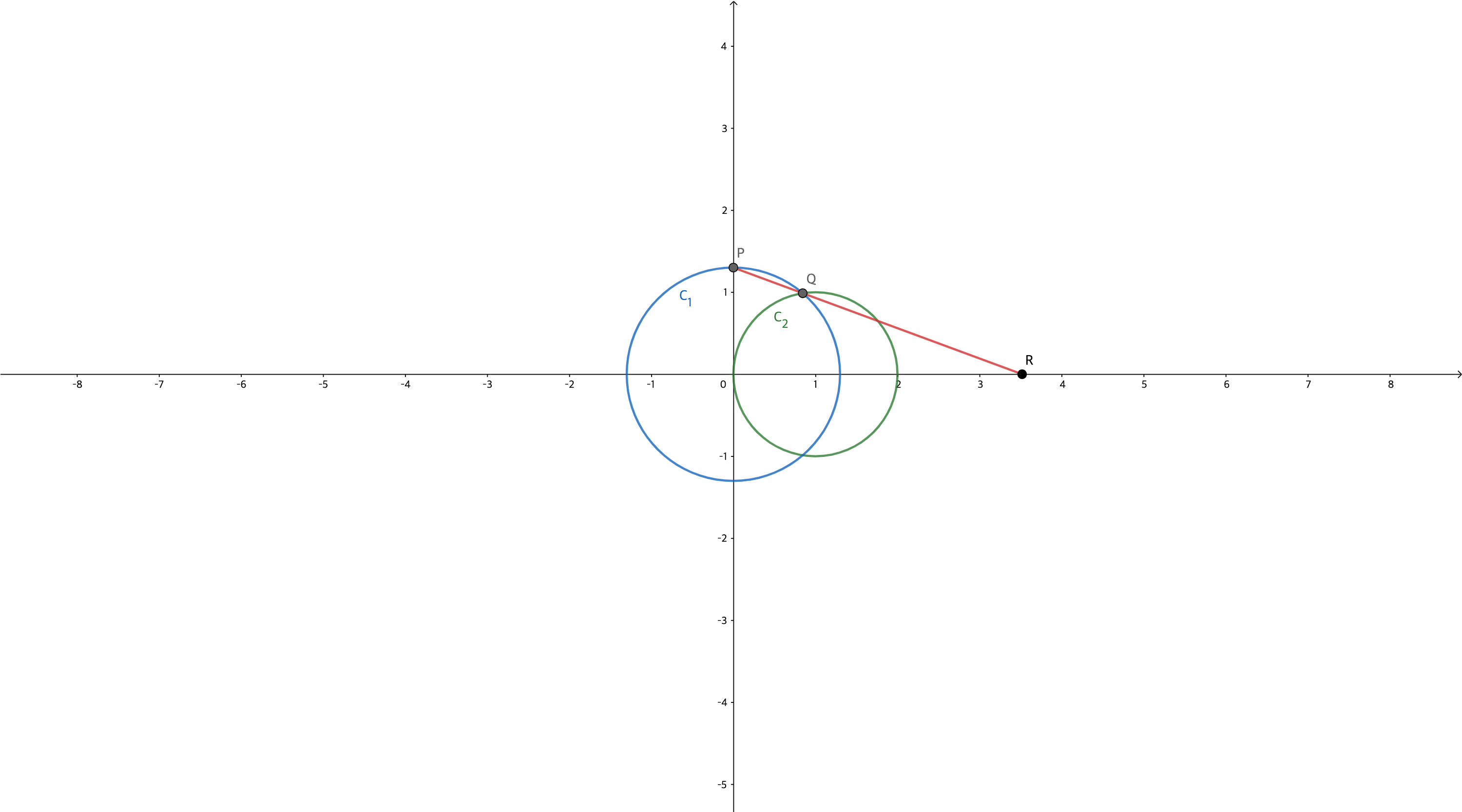
The figure shows a fixed circle \(C_{1}\) with equation \((x-1)^{2} + y^{2} = 1\) and a shrinking circle \(C_{2}\) with radius \(r\) and center the origin. \(P\) is the point \((0, r)\), \(Q\) is the upper point of intersection of the two circles, and \(R\) is the point of intersection of the line \(PQ\) and the x-axis. What happens to \(R\) as \(C_{2}\) shrinks, that is, as \(r\to{0^{+}}\)?

Answer

Answer 1

(a)

\[\frac{x^{2}+x-6}{x-2} \neq x + 3\] \[(\because \frac{x^{2}+x-6}{x-2} \text{ is not defined when x = 2})\]

(b)

\[\lim_{x\to{2}}\frac{x^{2} + x - 6}{x - 2} = \lim_{x\to{2}}\frac{(x-2)(x+3)}{x - 2}\] \[= \lim_{x\to{2}}(x + 3)\] \[(\because x\to{2} \text{ is not equal to }x=2)\]

Answer 2

\[\text{Since the denominator approaches 0 as } x\to{-2}\] \[\text{The limit will exist only if the nominator approaches 0 as } x\to{-2}\]

\[\lim_{x\to{-2}}{(3x^{2}+ax+a+3)} = 0\] \[3(-2)^2+a(-2)+a+3 = 0\] \[\therefore a = 15\]

\[\text{With } a = 15, \text{the limit becomes}\] \[\lim_{x\to{-2}}{\frac{3x^{2}+15x+18}{x^{2}+x-2}} = \lim_{x\to{-2}}{\frac{3(x+2)(x+3)}{(x-1)(x+2)}}\] \[= \lim_{x\to{-2}}{\frac{3(x+3)}{(x-1)}}\] \[(\because x\to{-2} \text{ is not equal to }x = -2)\] \[= \frac{3((-2)+3)}{((-2)-1)}\] \[= \frac{3}{(-3)} = -1\]

Answer 3

\[C_{1}: (x-1)^{2}+y^{2} = 1\] \[C_{2}: x^{2} + y^{2} = r\] \[\text{We already know the coordinates of the point P is } (0, r) \text{ from graph.}\] \[\text{Thus, we must first find the coordinates of the point } Q \text{ to get the equation of the line } PR.\] \[Q \text{ is the upper point of intersection of the two circles.}\]

\[\therefore x^{2} + 1 - (x-1)^{2} = r^{2}\] \[x = \frac{r^{2}}{2}\] \[x = \frac{r^{2}}{2} \text{ is the } x\text{-coordinate of the point Q.}\] \[\text{Substituting back into any equation of the two circles to find the } y\text{-coordinate}.\] \[(\frac{r^{2}}{2})^{2} + y^{2} = r^{2}\] \[y^{2} = r^{2} - (\frac{r^{2}}{2})^{2}\] \[y = \sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}\] \[(\because y \geq 0)\] \[\therefore y = \sqrt{r^{2}-(\frac{r^{2}}{2})^{2}} \text{ is the } y\text{-coordinate of the point Q.}\] \[\text{Now, The equation of the line joining } P \text{ and } Q \text{ is thus}\] \[y = -\frac{r-\sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}}{\frac{r^{2}}{2}}x + r\] \[\text{We set } y = 0 \text{ in order to find the x-intercept, and get}\] \[-\frac{r-\sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}}{\frac{r^{2}}{2}}x + r = 0\] \[x = \frac{-r^{3}}{-2r+2\sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}}\]

\[\text{Let's take the limit as } r\to{0^{+}}.\] \[\lim_{r\to{0^{+}}}\frac{-r^{3}}{-2r+2\sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}}\]

\[\lim_{r\to{0^{+}}}\frac{-r^{3}}{-2r+2\sqrt{r^{2}-(\frac{r^{2}}{2})^{2}}} = \lim_{r\to{0^{+}}}\frac{-r^{3}}{-2r(1-\sqrt{1-\frac{r^{2}}{4}})}\] \[= \lim_{r\to{0^{+}}}\frac{r^{2}}{2(1-\sqrt{1-\frac{r^{2}}{4}})} = \lim_{r\to{0^{+}}}\frac{r^{2}(1+\sqrt{1-\frac{r^{2}}{4}})}{2(1-\sqrt{1-\frac{r^{2}}{4}})(1+\sqrt{1-\frac{r^{2}}{4}})}\] \[= \lim_{r\to{0^{+}}}\frac{r^{2}(1+\sqrt{1-\frac{r^{2}}{4}})}{2\{1-(1-\frac{r^{2}}{4})\}} = \lim_{r\to{0^{+}}}\frac{r^{2}(1+\sqrt{1-\frac{r^{2}}{4}})}{\frac{r^{2}}{2}}\] \[= \lim_{r\to{0^{+}}}2(1+\sqrt{1-\frac{r^{2}}{4}}) = 4\]