Calculus: Applications of Differentiation - The Mean Value Theorem #3
Questions
Question 1
At 2:00 p.m. a car’s speedometer reads 50\(km/h\). At 2:20 p.m. it reads 65\(km/h\). Show that at some time between 2:00 and 2:20 the acceleration is exactly 45\(km/h^{2}\).
Let \(v(t)\) be the velocity of the car \(t\) hours after 2:00 p.m. Then \(\frac{v(1/3) - v(0)}{1/3 - 0} = ?\). By the Mean Value Theorem, there is a number \(c\) such that \(0 < c < ?\) with \(v^{'}(c) = ?\). Since \(v^{'}(t)\) is the acceleration at time \(t\), the acceleration \(c\) hours after 2:00 p.m. is exactly 45 \(km/h^{2}\).
Answers
Answer 1
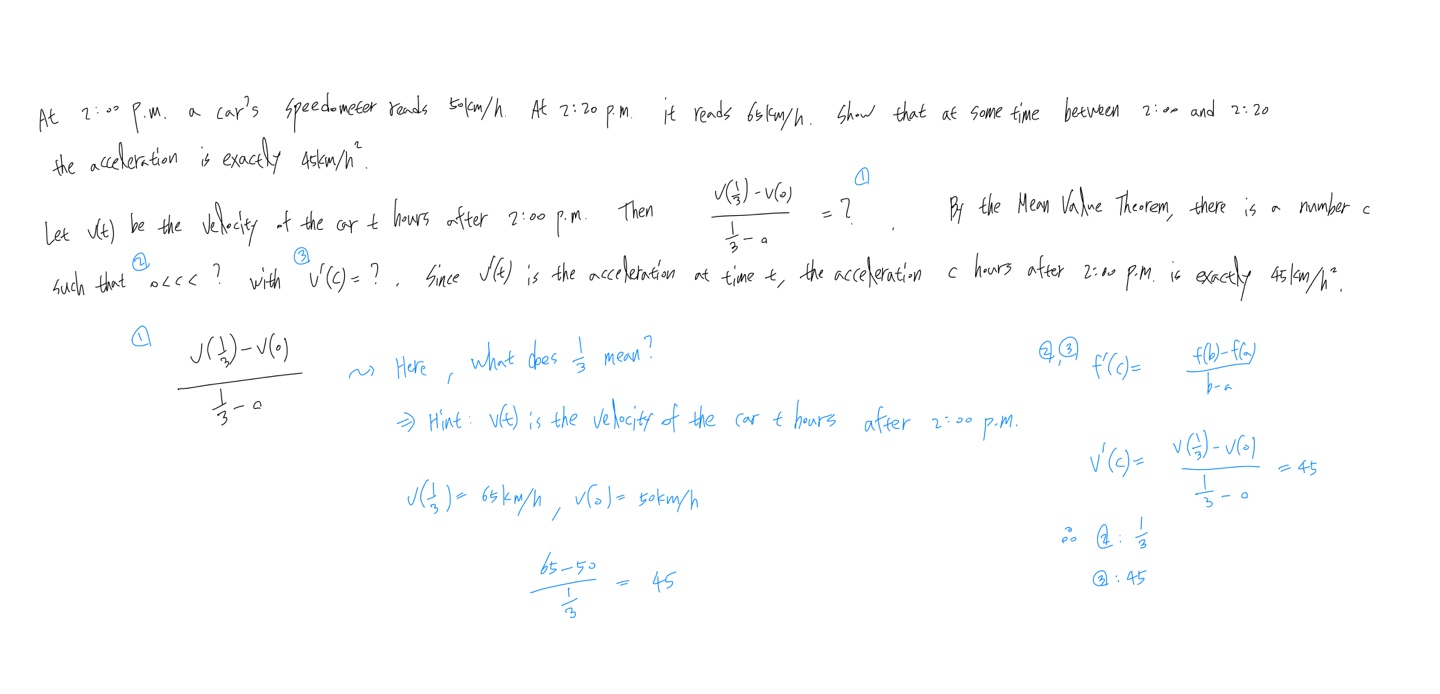

댓글남기기