Calculus: Applications of Differentiation - The Mean Value Theorem #1

Concepts

The Mean Value Theorem

Lef \(f\) be a function that satisfies the following hypotheses:

1. \(f\) is continuous on the closed interval \([a, b]\).
2. \(f\) is differentiable on the open interval \((a, b)\).

Then there is a number \(c\) in \((a, b)\) such that

\[f^{'}(c) = \frac{f(b) - f(a)}{b - a}\]

or, equivalently,

\[f(b) - f(a) = f^{'}(c)(b - a)\]

Questions

Consider the following function and closed interval.

\[f(x) = x^{3} - 3x + 4, [-2, 2]\]

Question 1

Find \(\frac{f(b) - f(a)}{b - a}\) for \([a, b] = [-2, 2]\). (If an answer does not exist, enter DNE.)

\[\frac{f(b) - f(a)}{b - a} = ?\]

Question 2

If the mean value theorem can be applied, find all values of \(c\) that satisfy the conclusion of the mean value theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE).

\[c = ?\]

Answers

Answer 1

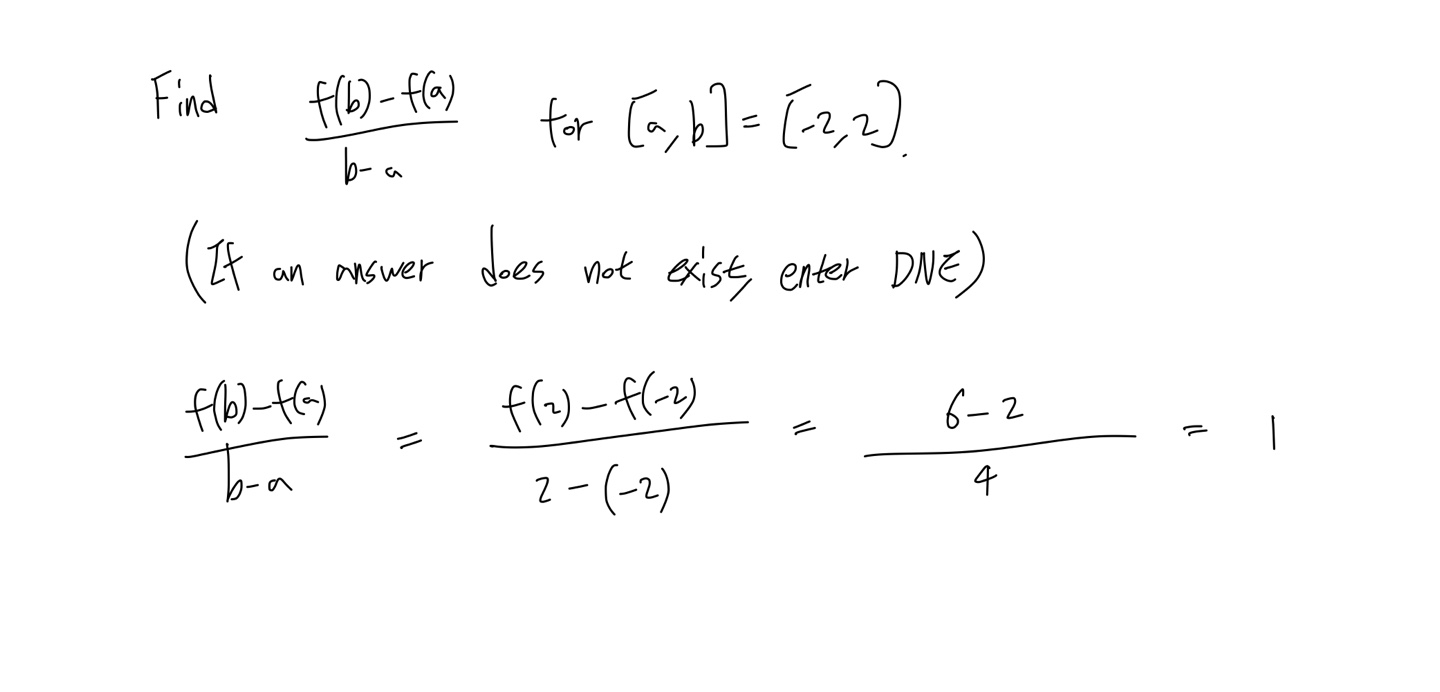
Answer 2